Dans la vie de tous les jours, nous utilisons le langage décimal pour compter.
Il est également appelé système de numération en base 10.
Il est composé de dix chiffres (qui sont 1,2,3,4,5,6,7,8,9 et 0), avec lesquels nous pouvons écrire n’importe quel nombre en base 10.
Prenons un nombre en base 10 : (9825)10
Il peut se décomposer comme cela :
5 * 10 ^ 0 = 5 * 1 = 5
+ 2 * 10 ^ 1 = 2 * 10 = 20
+ 8 * 10 ^ 2 = 8 * 100 = 800
+ 9 * 10 ^ 3 = 9 * 1000 = 9000
= (9825)10
L’électronique digitale travaille avec deux états : 0 ou 1
- 0 est une absence de signal ( 0 volt)
- 1 est une présence de signal ( 5 Volts ou 3.33 volts)
Cette numération composée de 0 et de 1 est appelée langage binaire ou système de numération en base 2.
Les processeurs qui sont composés d’électronique digitale utilisent donc deux chiffres : 0 et 1, toutes les informations et instructions gérées par ceux-ci sont donc uniquement composées de 0 et de 1.
Comment peut-on décoder un nombre en base 2 :
Prenons un nombre en base 2 : (10110011)2
Il peut se décomposer comme cela :
1 * 2 ^ 0 = 1 * 1 = 1
+ 1 * 2 ^ 1 = 1 * 2 = 2
+ 0 * 2 ^ 2 = 0 * 4 = 0
+ 0 * 2 ^ 3 = 0 * 8 = 0
+ 1 * 2 ^ 4 = 1 * 16 = 16
+ 1 * 2 ^ 5 = 1 * 32 = 32
+ 0 * 2 ^ 6 = 0 * 64 = 0
+ 0 * 2 ^ 7 = 1 * 128 = 128
= (179)10
Les 0 et 1 sont appelés des Binary Digits ou bits
8 bits = 1 octet
Un octet permet de coder des nombres décimaux de :
(00000000)2 à (11111111)2
(0)10 à (255)10
Comment passer de la base 10 à la base 2 :
A ) La première méthode, « intuitive », consiste en fait à trouver de quelles puissances successives de 2 le nombre à convertir est formé, en commençant par la plus grande possible.
Il est dès lors pratique d’avoir sous la main un tableau des puissances consécutives de 2, avec leur rang correspondant :

Exemple :
(365)10
365 – 256 = 109 = 2 ^ 8
109 – 64 = 45 = 2 ^ 6
45 – 32 = 13 = 2 ^ 5
13 – 8 = 5 = 2 ^ 3
5 – 4 = 1 = 2 ^ 2
1 = 2 ^ 0
Résultat : (101101101)2
B) La seconde méthode que nous utiliserons pour convertir un nombre de base décimale en base binaire est la méthode des divisions.
Elle pourra d’ailleurs être utilisée de manière générale pour toutes les conversions entre bases.
Dans cette méthode, nous effectuerons des divisions successives par la base vers laquelle nous voulons convertir le nombre. Les restes successifs de ces divisions, notés dans l’ordre inverse de leurs apparitions, donnent le nombre exprimé dans la base désirée.
Exemple simple : convertir 13 en base 2.
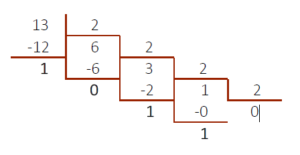
Les restes successifs des divisions par deux (1, 0, 1, 1), pris dans l’ordre inverse (1, 1, 0, 1), nous fournissent le développement en base deux du nombre 13 : (13)10 = (1101)2. On aurait aussi pu s’abstenir de faire la dernière division : diviser 1 par 2 fera toujours 0 (reste 1).Donc, nous prendrons directement le résultat de la division précédente.